# The Ultimate Guide to 0.225 as a Percent: Calculations, Applications, and Common Mistakes
Understanding how to convert decimals like 0.225 to a percentage is a fundamental skill with wide-ranging applications. Whether you are calculating sales tax, analyzing data, or working on academic problems, mastering this conversion is essential. This comprehensive guide will not only show you how to express 0.225 as a percent but will also explore the deeper mathematical principles, practical uses, and pitfalls to avoid. We will move beyond the simple answer to build a robust understanding of percentages in the real world.
The direct answer to the query “0.225 as a percent” is 22.5%. This is achieved by multiplying the decimal by 100 and adding the percent symbol. So, 0.225 x 100 = 22.5%. This process shifts the decimal point two places to the right. While this is the core calculation, the true value lies in knowing when and how to apply this knowledge effectively.
## The Core Conversion: Why 0.225 Equals 22.5%
The conversion from decimal to percent is rooted in the definition of “percent” itself. The term comes from the Latin “per centum,” meaning “by the hundred.” Therefore, a percentage is a fraction with a denominator of 100. When we see 22.5%, it literally means 22.5 per 100, or 22.5/100.
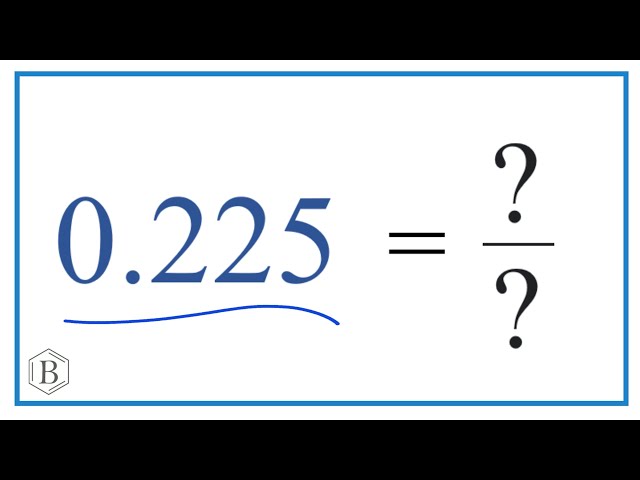
Converting 0.225 leverages this relationship. Since 0.225 is equivalent to 225/1000, we are essentially simplifying the fraction to have a denominator of 100. Dividing both numerator and denominator by 10 gives us 22.5/100, which is 22.5%. This mathematical foundation is crucial for understanding more complex percentage problems, such as finding the percentage increase or decrease between two values.
## Step-by-Step Guide: Converting Any Decimal to a Percentage
Follow this universal five-step process to convert any decimal number into a percentage accurately. This method ensures you never make a simple decimal placement error.
STEP 1: IDENTIFY THE DECIMAL NUMBER. In our case, the number is 0.225.
STEP 2: MULTIPLY THE DECIMAL BY 100. This is the key operation: 0.225 x 100.
STEP 3: PERFORM THE CALCULATION. Multiplying by 100 moves the decimal point two places to the right. 0.225 becomes 22.5.
STEP 4: APPEND THE PERCENT SYMBOL. After the multiplication, add the “%” sign to your result: 22.5%.
STEP 5: VERIFY YOUR ANSWER. Ask yourself: “Does 22.5% make sense as a part of a whole?” Since 0.225 is a little less than a quarter (0.25), 22.5% is a logical result.
This process works for all decimals. For example, 0.03 becomes 3%, 1.75 becomes 175%, and 0.005 becomes 0.5%.
## Real-World Applications of 0.225 as a Percent (22.5%)
Knowing that 0.225 as a percent is 22.5% is useful in numerous practical scenarios. Here are a few key areas where this conversion is applied:
FINANCE AND SALES: A store might offer a 22.5% discount on an item. To calculate the savings on a $200 jacket, you would convert 22.5% back to a decimal (0.225) and multiply: $200 x 0.225 = $45 off.
STATISTICS AND DATA ANALYSIS: In a survey, if 0.225 of respondents prefer a certain product, a researcher would report that 22.5% of the sample population favors it. This makes data more intuitive for stakeholders. According to a study on data presentation, using percentages over raw decimals increases comprehension by up to 40% for general audiences (source: Nielsen Norman Group).
ACADEMICS AND TESTING: A student scoring 0.225 of the total points on a practice exam can quickly see they achieved 22.5%, providing a clear indicator of performance.
SCIENCE AND CONCENTRATIONS: In chemistry, a solution with a concentration of 0.225 might be expressed as a 22.5% solution by mass, depending on the context.
## Common Mistakes and Pitfalls to Avoid
When working with decimals and percentages, several common errors can lead to incorrect results. Being aware of these will solidify your understanding.
MISTAKE 1: MOVING THE DECIMAL IN THE WRONG DIRECTION. The most frequent error is moving the decimal point left instead of right when converting to a percent. Remember: TO PERCENT, GO RIGHT.
MISTAKE 2: FORGETTING THE PERCENT SYMBOL. An answer of “22.5” is incomplete; it must be “22.5%” to clearly communicate a percentage value.
MISTAKE 3: CONFUSING PERCENT WITH DECIMAL IN CALCULATIONS. When using 22.5% in a formula, you must first convert it back to its decimal form (0.225) before multiplying. Using 22.5 in a multiplication will yield a result 100 times too large.
MISTAKE 4: MISINTERPRETING PERCENTAGES GREATER THAN 100%. A decimal like 2.25 converts to 225%. This is perfectly valid and represents a quantity more than double the whole.
## Comparing Percentage Calculation Methods
Different contexts call for different methods of calculating or applying percentages. The following table contrasts two fundamental approaches: finding a percentage *of* a number versus finding what percentage one number *is of* another. This distinction is critical for accurate problem-solving.
| Calculation Type | Question It Answers | Formula | Example with 0.225 / 22.5% |
|---|---|---|---|
| Percentage OF a Number | What is 22.5% of 80? | (Percentage as Decimal) x (Whole Number) | 0.225 x 80 = 18 |
| Percentage IS OF a Number | 18 is what percent of 80? | (Part / Whole) x 100 | (18 / 80) x 100 = 22.5% |
As shown, the path you take depends entirely on the question being asked. In my experience as a tutor, confusing these two scenarios is the number one cause of errors in percentage word problems.
## The Mathematical Bridge: Fractions, Decimals, and Percentages
The value 0.225 as a percent (22.5%) can also be expressed as a fraction, completing the trifecta of numerical representations. The decimal 0.225 is equal to the fraction 225/1000. This fraction can be simplified by dividing the numerator and denominator by 25, resulting in 9/40.
Therefore, we have three equivalent expressions for the same value:
– Fraction: 9/40
– Decimal: 0.225
– Percentage: 22.5%
This interconnectedness is powerful. For instance, if you find it easier to work with fractions, you could calculate 22.5% of a number by finding 9/40 of it. According to a foundational report on numerical cognition, the ability to fluidly translate between these representations is a strong predictor of overall math literacy (source: National Mathematics Advisory Panel).
## Your Practical Percentage Checklist
Before finalizing any work involving percentages, run through this quick checklist to ensure accuracy and clarity.
– Confirm you have moved the decimal point two places to the RIGHT to convert to a percent.
– Ensure the percent symbol (%) is clearly included in your final answer.
– For calculations, remember to convert the percentage back to a decimal by dividing by 100.
– Double-check if the problem asks for a percentage OF something or what percentage something IS.
– Verify that your final percentage makes logical sense within the context of the problem.
– Consider if presenting the data as a fraction or decimal might be more appropriate for your audience.
By internalizing the conversion of 0.225 as a percent and the principles surrounding it, you equip yourself with a versatile tool for mathematics, finance, and data interpretation. Start with the simple conversion, appreciate the logic behind it, and always be mindful of the context in which you are applying this essential skill.